知识蒸馏

模型知识蒸馏相关知识点总结，包括实现流程，作用，分类等。持续更新中…

• Model Distillation

  模型蒸馏（Model Distillation）最初由Hinton等人在2015年提出，其核心思想是通过知识迁移的方式，将一个复杂的大模型（教师模型）的知识传授给一个相对简单的小模型（学生模型）

  简单概括就是利用教师模型的预测概率分布作为**软标签**对学生模型进行训练，从而在保持较高预测性能的同时，极大地降低了模型的复杂性和计算资源需求，实现模型的轻量化和高效化。

  1. 实现流程

  ​

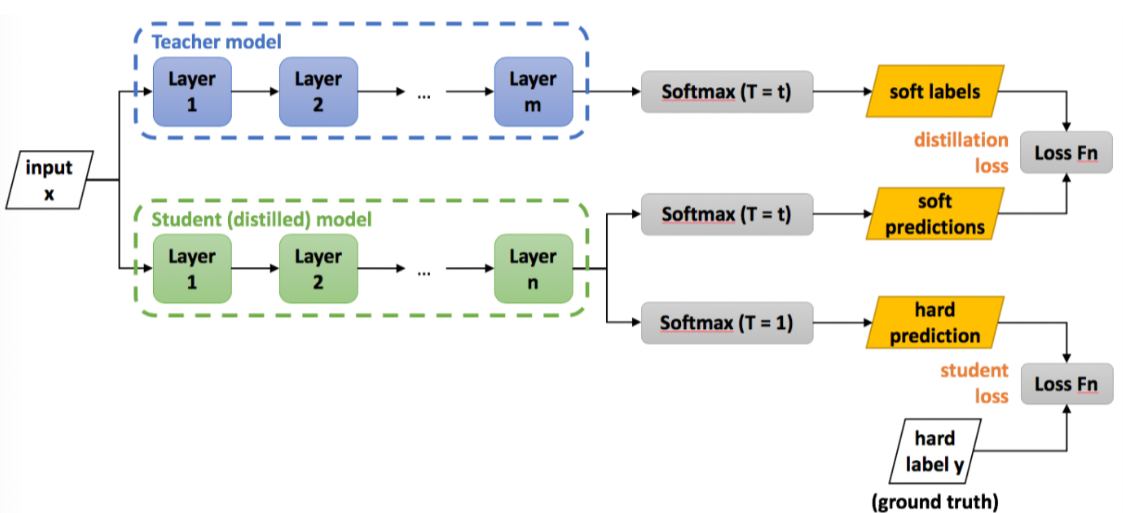
  1. 准备教师模型和学生模型

     首先，我们需要一个已经训练好的教师模型和一个待训练的学生模型。教师模型通常是一个性能较好但计算复杂度较高的模型，而学生模型则是一个计算复杂度较低的模型。

  2. 使用教师模型对数据集进行预测

     得到每个样本的预测概率分布（软目标）。这些概率分布包含了模型对每个类别的置信度信息。

  3. 定义损失函数

     损失函数用于衡量学生模型的输出与教师模型的输出之间的差异。在模型蒸馏中，我们通常会使用一种结合了==软标签损失Distillation Loss==和==硬标签损失Student Loss==的混合损失函数（通常这两个损失都可以看作交叉熵损失）。软标签损失鼓励学生模型模仿教师模型的输出概率分布，这通常使用 KL 散度（Kullback-Leibler Divergence）来度量，而硬标签损失则鼓励学生模型正确预测真实标签。

     其中，软标签损失$\text{SoftLoss} = \frac{1}{T^{2}} \sum_{i=1}^{C} q_{i} \log \left( \frac{q_{i}}{p_{i}} \right)$，硬标签损失（交叉熵）$\text{HardLoss} = -\sum_{i=1}^{C} y_{i} \log\left(p_{i}\right)$
     总损失为$\text{TotalLoss} = \alpha \cdot \text{SoftLoss} + (1 - \alpha) \cdot \text{HardLoss}$

     KL散度（Kullback-Leibler divergence）

     可以以称作相对熵（relative entropy）或信息散度（information divergence）。

     $KL(p|q)$表示用分布 $q$ 拟合分布 $p$ 带来的误差。其中 $p$ 是输出的真实分布，我们的数据集的标签 $y$ 就从这个分布中采样而来。
     对于一个 $K$ 分类问题， $y_i$ 常常会表示为one-hot向量，包含1个1和 $K - 1$ 个0。对于模型蒸馏，损失函数可以表示为 $KL(q_t||q_s)$ ，
     表示用学生模型的输出 $q_s$ 来拟合教师模型的输出 $q_t$ 。

     KL散度的理论意义在于度量两个概率分布之间的差异程度，当KL散度越大的时候，说明两者的差异程度越大；而当KL散度小的时候，则说明两者的差异程度小。
     如果两者相同的话，则该KL散度应该为0。

  4. 训练学生模型

     在训练过程中，我们将教师模型的输出作为监督信号，通过优化损失函数来更新学生模型的参数。这样，学生模型就可以从教师模型中学到有用的知识。
     KL 散度的计算涉及一个温度参数，该参数可以调整软目标的分布。温度较高会使分布更加平滑。在训练过程中，可以逐渐降低温度以提高蒸馏效果。

     蒸馏中的温度（Softmax With Temperature）

     为什么需要温度系数？

     模型在训练收敛后，往往通过softmax的输出不会是完全符合one-hot向量那样极端分布的，而是在各个类别上均有概率，推断时通过argmax取得概率最大的类别。
     Hinton的文章指出，教师模型中在这些负类别上输出的概率分布包含了一定的隐藏信息。比如MNIST手写数字识别，标签为7的样本在输出时，类别7的概率虽然最大，但和类别1的概率更加接近，这就说明1和7很像，这是模型已经学到的隐藏的知识。
     我们在使用softmax的时候往往会将一个差别不大的输出变成很极端的分布，导致类别间的隐藏的相关性信息不再那么明显，为了解决这个问题，我们就引入了温度系数。

     如何使用温度？

     下图最左侧是我们数据的原始分布，右侧分别展示了不同温度系数下的分布情况。可以看出，高温的分布均匀，低温的分布尖锐，T=1.0时输出为softmax输出分布。
     引入温度系数的本质目的，就是让softmax的soft程度变成可以调节的超参数。
     如果是模型蒸馏， $L_1$ 项始终都使用较大的温度；如果是使用真实标签训练，确实选取较小的温度系数，更利于模型收敛。
     可以这样理解，温度系数较大时，模型需要训练得到一个很陡峭的输出，经过softmax之后才能获得一个相对陡峭的结果；温度系数较小时，模型输出稍微有点起伏，softmax就很敏感地把分布变得尖锐，认为模型学到了知识。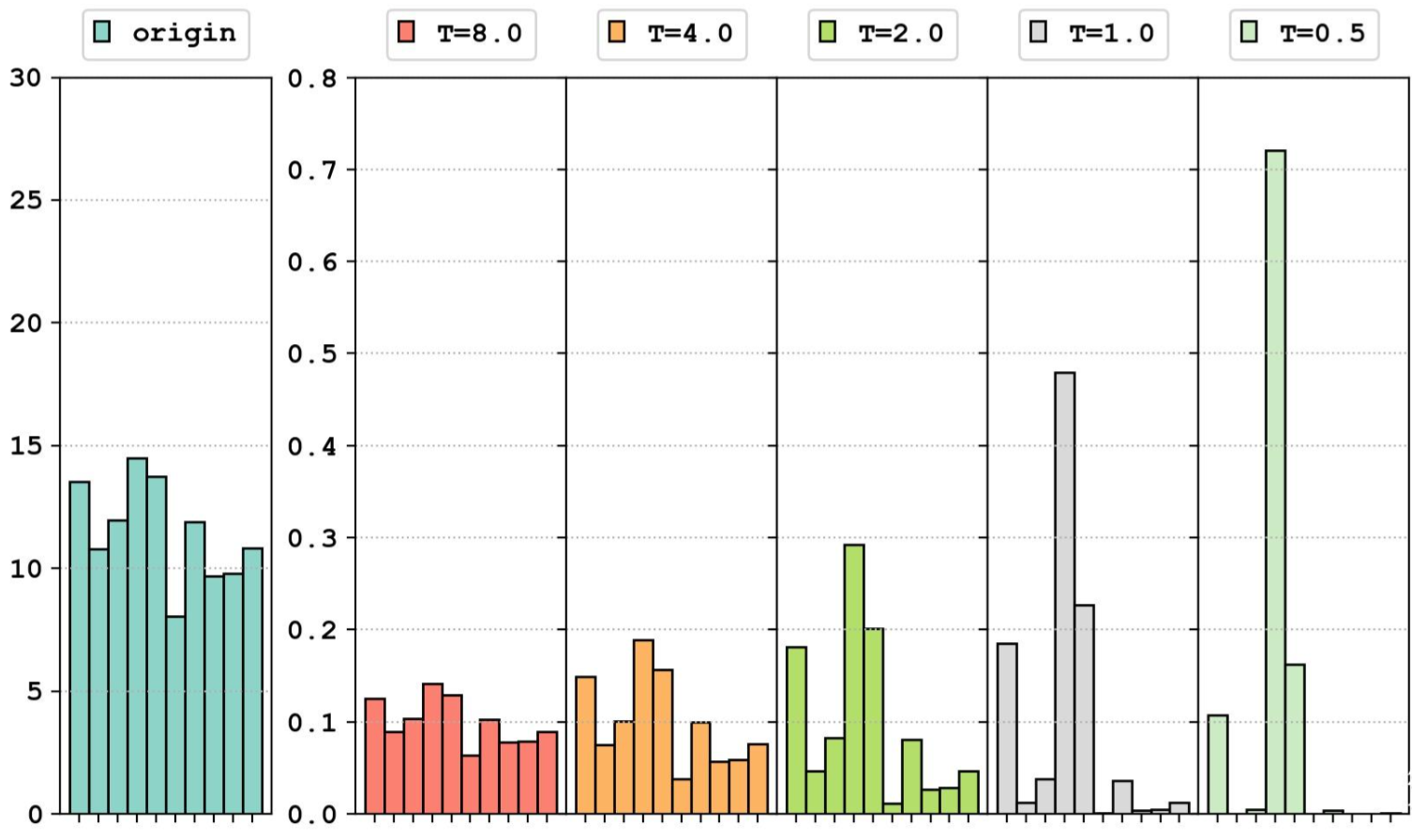

     ​

  5. 微调学生模型

     在蒸馏过程完成后，可以对学生模型进行进一步的微调，以提高其性能表现。

  ‍

  2. 作用

  1. 模型轻量化：通过将大型模型的知识迁移到小型模型中，可以显著降低模型的复杂度和计算量
  2. 降本增效：运行时速度更快，降低了计算成本和能耗，进一步的，减少了对硬件资源的需求，降低模型运行成本
  3. 泛化能力：模型蒸馏可能帮助学生模型学习到教师模型中蕴含的泛化模式，提高其在未见过的数据上的表现

  ‍

  3. 分类

  我们在实现流程中介绍的是蒸馏技术的一种，基于响应的软标签知识蒸馏。这是最早期、最经典也是最常用的一种蒸馏方式。
  但Response-Based的知识来源单一，只利用了模型的最后一层信息，忽略了网络中间层包含的大量丰富的特征信息。
  基于特征的知识蒸馏可以弥补这种缺陷

  1. Feature-Based Knowledge Distillation

     Feature-based 蒸馏让学生模型模仿教师模型中间层的特征表示，中间层特征保留更多结构与空间信息，早期层能引导学生捕捉关键模式，适用于目标检测、分割等任务

     但教师和学生结构差异大时对齐较难，且特征对齐会增加内存和训练复杂度

     • FitNets: Hints for Thin Deep Nets （Romero et al., ICLR 2015）

       • 动机：

         人们发现直接训练一个又深又窄的学生网络非常困难，因为它梯度传播路径长，容易出现梯度消失/爆炸。同时，仅仅用最终的软标签来指导它，对网络前、中段的层来说，监督信号太间接、太弱了。学生网络不知道如何正确地初始化和学习其早期层。

       • 方法：

         FitNets巧妙地将训练过程分为两个阶段，引入了“提示”（Hint）的概念：

         1. 提示训练(Hint-based Training)

            从教师模型中选择一个中间层（称为Hint层），并从学生模型中选择一个相对较深的中间层（因为学生网络更窄，需要更深才能达到相似的表征能力）
            由于学生和老师的特征图通道数、尺寸可能不同，在学生模型的Hint层后面加了一个卷积回归器（regressor），将学生的特征图在形状上匹配到老师的特征图
            此阶段，只训练学生模型从输入层到Hint层以及回归器部分的参数。网络后面的部分不参与训练。这相当于在老师的指导下，先把学生网络的前半部分“扶上正轨”

         2. 完整知识蒸馏训练 (Full Distillation Training)

            在学生网络前半部分被预训练好之后，丢弃那个临时的回归器。
            用经典的基于响应的知识蒸馏来训练整个学生网络。即，总损失 = 蒸馏损失 (软标签) + 学生损失 (硬标签)

     • Attention Transfer（Zagoruyko & Komodakis, 2017）

       • 动机：

         FitNets强制学生模仿老师完整的特征图，这可能过于严苛和冗余。特征图中真正重要的是模型“关注”的空间区域。
         比如在识别一只鸟时，网络应该更关注鸟本身，而不是背景的天空。这种“注意力”信息比像素级的特征值更抽象，也更关键。

       • 方法：

         AT的核心是让学生模仿老师的注意力图（Attention Map）

         1. 定义注意力图

            如何从一个普通的特征图中提取注意力图？作者提出了一种简单而有效的方法：计算特征图在通道维度上的统计量。
            具体来说，可以将一个形状为 [C, H, W] 的特征图，通过计算每个空间位置(h, w)上所有通道激活值的p范数（通常用L2范数），来生成一个 [H, W] 的注意力图。这个图的每个像素值代表了模型在该空间位置的“关注强度”。

            $AttentionMap(h, w) = || FeatureMap[:, h, w] ||_p$

         2. 传递注意力

            在教师和学生网络的对应阶段（例如，每个ResNet block的输出），分别生成注意力图
            蒸馏损失被定义为教师和学生的**注意力图之间的L2距离**。为了让不同尺度的注意力图具有可比性，通常会先对其进行归一化
            这个注意力损失可以与经典的蒸馏损失和分类损失结合在一起，进行端到端的训练

  2. Relation-based Knowledge Distillation

     前面提到响应蒸馏关注预测结果，特征蒸馏关注中间层特征表示
     而关系蒸馏认为，孤立的特征值或预测值不是最重要的，最重要的是样本之间、或者特征之间的相互关系。学生应该学习老师是如何组织和看待整个数据流形结构的。
     这种方法关注的是 样本之间 / 通道之间 / 空间之间的结构组织信息，例如“哪些样本更相似”。

     • Relational Knowledge Distillation (RKD) (Park et al., CVPR 2019)

       • 动机

         直接匹配特征（如FitNets）可能会因为教师和学生的能力差异（Capacity Gap）而受限。一个简单的学生模型可能永远无法完美复现复杂教师模型的特征。
         RKD提出，我们不需要模仿特征本身，只需要模仿数据样本在特征空间中的相对关系。

       • 方法

         RKD在一个mini-batch的数据内，构建样本间的关系，并让学生模仿。

         1. 提取特征: 从一个包含N个样本的批次中，分别提取教师和学生的特征嵌入（embeddings），得到教师的特征集${t_1, t_2, …, t_N}$ 和学生的特征集${s_1, s_2, …, s_N}$

         2. 定义关系损失

            距离关系: 计算批次内每两个样本特征之间的欧氏距离，形成一个N x N的距离矩阵。让学生的距离矩阵与老师的距离矩阵尽可能相似；
            角度关系: 计算批次内每两个样本特征向量之间的夹角（余弦相似度）。形成一个 N x N 的角度矩阵。让学生的角度矩阵与老师的角度矩阵相似。

         使用Huber损失来计算教师和学生关系矩阵之间的差异

‍